Transformar decimal a fracción
Los números decimales pueden clasificarse en:
a) decimales finitos: son aquellos que tienen fin, es decir, no hay un número que se repita.
Ejemplos: 4,56 ; 0,0003 ; 2,9876 : 0,1 ; 3,42 , etc.
Siempre que se divida el numerador por el denominador, y la división termine y se obtenga resto cero, la división es exacta y su resultado será un decimal finito.
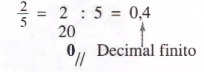
b) decimales infinitos: son aquellos números que no se acaban, es decir, hay uno o varios números que se repiten infinitamente. Por ejemplo: 0,333333..... es infinito por que el 3 se repite indefinidamente. Estos números son divisiones inexactas. No representan una fracción decimal.

Al conjunto de los números racionales sólo pertenecen los números decimales infinitos periódicos y semiperiódicos. Los decimales infinitos puros pertenecen al conjunto de los números irracionales, porque no pueden transformarse en fracción.
c) decimales infinitos periódicos: son aquellos que tiene una o más cifras que se repiten sucesiva e infinitamente, formando el período. Se escribe en forma abreviada coronando al período con un pequeño trazo.


Se convierte el número a fracción decimal y, si se puede, se simplifica. Para transformar el número decimal a fracción decimal se utilizan potencias de diez (10, 100, 1.000, etc.). Se colocan tantos ceros como cifras decimales tenga el número.
Ejemplo 1:
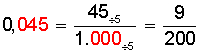
Ejemplo 2:
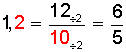
Transformación de un decimal infinito
periódico en fracción
Los pasos a seguir son los siguientes:1) Se anota el número y se le resta él o los números que están antes del período (de la rayita)
2) Se coloca como denominador un 9 por cada número que está en el período (si hay un número bajo la rayita se coloca un 9, si hay dos números bajo el período se coloca 99, etc.). Si se puede simplificar, se simplifica.
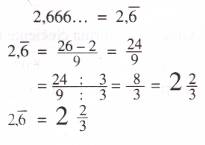
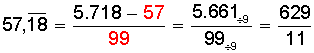
Transformación de decimal infinito semiperiódico a fracción
1)
El numerador de la fracción
se obtiene, al igual que en el caso anterior,
restando al número la parte entera y el anteperíodo, o sea, todo lo que
está antes de la “rayita”.
2) El
denominador de la fracción se obtiene colocando
tantos 9 como cifras tenga el período
y tantos 0 como cifras tenga el anteperíodo.
Como siempre, el resultado se expresa como fracción irreductible (no se
puede simplificar más) o como número mixto.
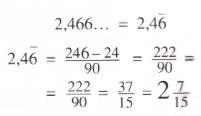
Convertir Decimales a Fracciones
Para convertir un Decimal a una Fracción sigue estos pasos:
| Paso 1: Escribe el decimal dividido por 1. |
| Paso 2: Multiplica los números de arriba y abajo por 10 una vez por cada número luego de la coma. (Por ejemplo, si hay dos números luego del decimal, multiplícalos por 100, si hay tres usa el 1000, etc.) |
| Paso 3: Simplifica (reduce) la fracción |
Ejemplo 1: Expresar 0,75 como fracción
Paso 1: Escribe:| 0,75 |
| 1 |
| × 100 | ||
| 0,75 | = | 75 |
| 1 | 100 | |
| × 100 | ||
(¿Ves como el número de arriba se convierte
en un entero?)
Paso 3: Simplifica la fracción:en un entero?)
| ÷ 25 | ||
| 75 | = | 3 |
| 100 | 4 | |
| ÷ 25 | ||
Respuesta = 3/4
Nota: ¡75/100 se llama una fracción
decimal y 3/4 es llamada una fracción común !
Ejemplo 2: Expresa 0,625 como una fracción
Paso 1: escribe:| 0,625 |
| 1 |
| 625 |
| 1.000 |
| ÷ 25 | ÷ 5 | |||
| 625 | = | 25 | = | 5 |
| 1,000 | 40 | 8 | ||
| ÷ 25 | ÷ 5 | |||
Respuesta = 5/8
Ejemplo 3: Expresa 0,333 como fracción
Paso 1: Escribe abajo:| 0,333 |
| 1 |
| 333 |
| 1.000 |
¡No se puede simplificar!
Respuesta = 333/1000
Pero una Nota Especial:
Si en realidad quieres expresar 0,333... (en otras palabras los 3 repitiéndose para siempre lo que se llama 3 periódico) entonces necesitas seguir un argumento especial. En este caso escribimos:| 0,333... |
| 1 |
| × 3 | ||
| 0,333... | = | 0,999... |
| 1 | 3 | |
| × 3 | ||

No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.